Branches and Binary Operators

BOA: Branches and Binary Operators

Next, lets add

• Branches (if-expressions)
• Binary Operators (+, -, etc.)

In the process of doing so, we will learn about

• Intermediate Forms
• Normalization

Branches

Lets start first with branches (conditionals).

We will stick to our recipe of:

1. Build intuition with examples,
2. Model problem with types,
3. Implement with type-transforming-functions,
4. Validate with tests.

data Expr = ENum                  -- 12 
          | EPrim1 Op1  Expr      -- add1(e)
          | EVar   Id             -- x
          | ELet   Id   Expr Expr -- let x = e1 in e2
          | EIf    Expr Expr Expr

Examples

First, lets look at some examples of what we mean by branches.

• For now, lets treat 0 as “false” and non-zero as “true”

Example: If1

if 10:
  22
else:
  sub1(0)

• Since 10 is not 0 we evaluate the “then” case to get 22

Example: If2

if sub(1):
  22
else:
  sub1(0)

• Since sub(1) is 0 we evaluate the “else” case to get -1

QUIZ: If3

if-else is also an expression so we can nest them:

What should the following evaluate to?

let x = if sub(1):
          22
        else:
          sub1(0)
in
  if x:
    add1(x)
  else:
    999

• A. 999
• B. 0
• C. 1
• D. 1000
• E. -1

Control Flow in Assembly

To compile branches, we will use:

• labels of the form

our_code_label:
  ...

are “landmarks” from which execution (control-flow) can be started, or to which it can be diverted,

• comparisons of the form

cmp a1, a2

• Perform a (numeric) comparison between the values a1 and a2, and

• Store the result in a special processor flag,

• Jump operations of the form

jmp LABEL     # jump unconditionally (i.e. always)
je  LABEL     # jump if previous comparison result was EQUAL  
jne LABEL     # jump if previous comparison result was NOT-EQUAL  

• Use the result of the flag set by the most recent cmp
• To continue execution from the given LABEL

QUIZ

Which of the following is a valid x86 encoding of

if 10:
  22
else
  33

Strategy

To compile an expression of the form

if eCond:
  eThen
else:
  eElse

We will:

1. Compile eCond
2. Compare the result (in eax) against 0
3. Jump if the result is zero to a special "IfFalse" label
   • At which we will evaluate eElse,
   • Ending with a special "IfExit" label.
4. (Otherwise) continue to evaluate eTrue
   • And then jump (unconditionally) to the "IfExit" label.

Example: If-Expressions to Asm

Lets see how our strategy works by example:

Example: if1

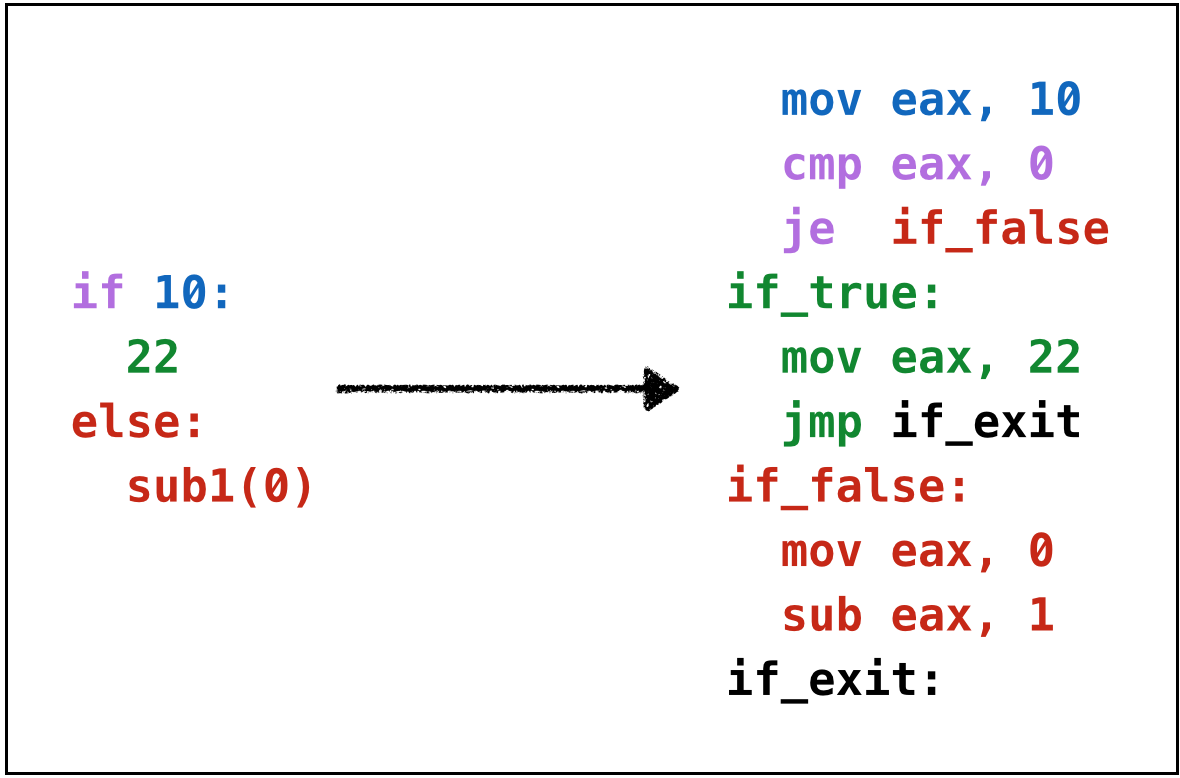
Example: if2

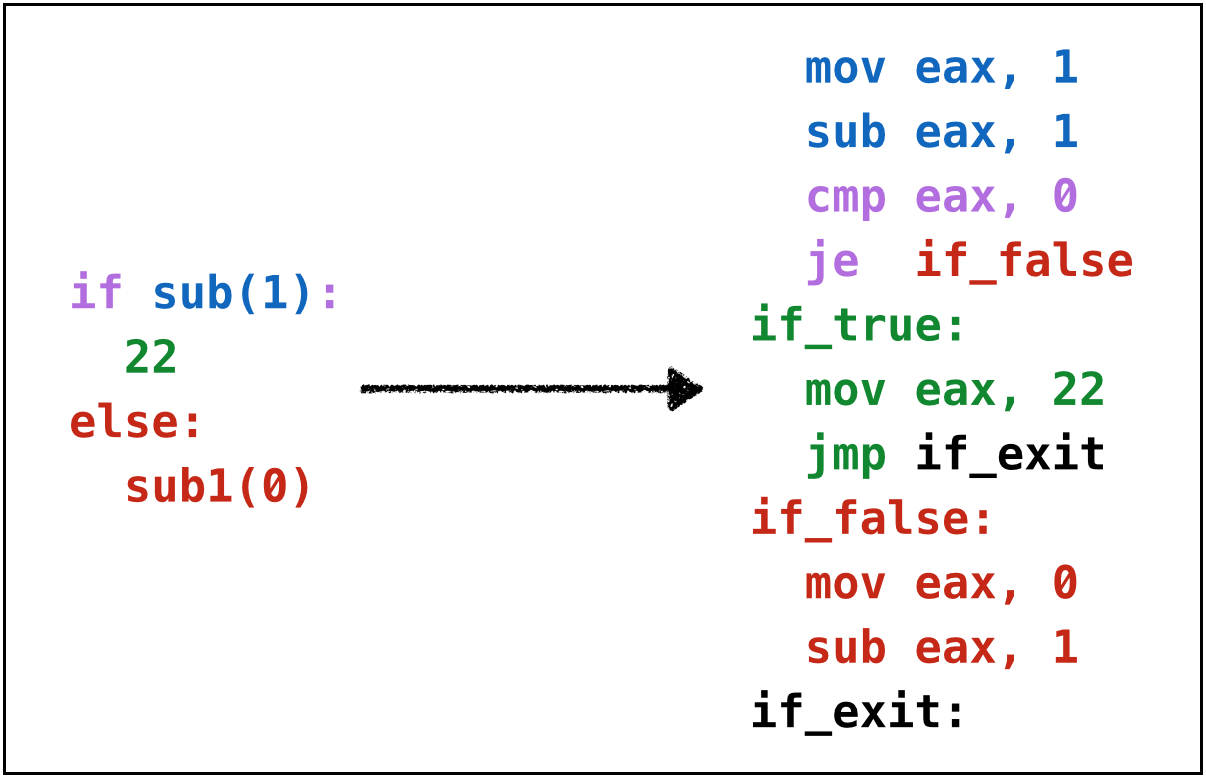
Example: if3

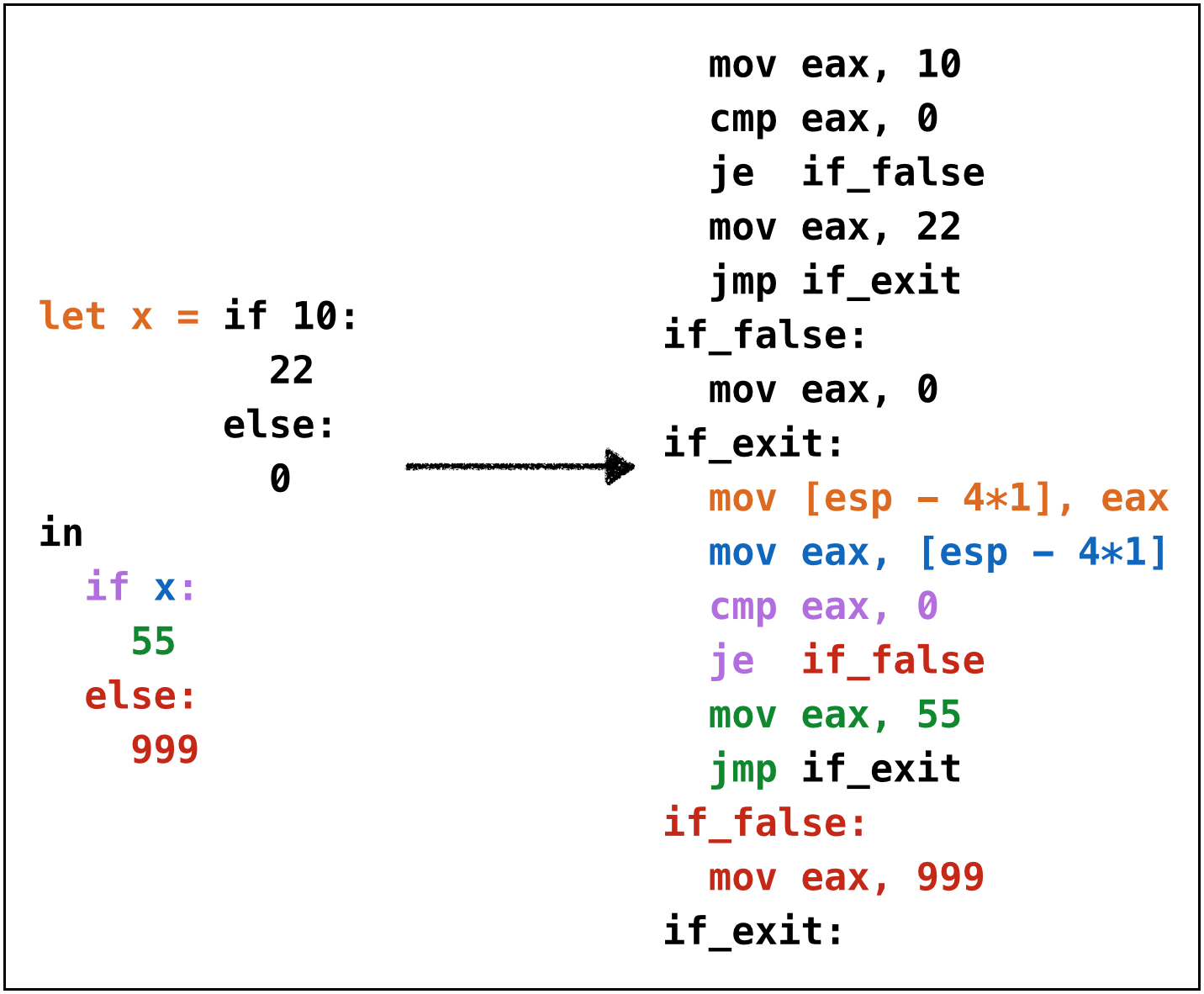
Oops, cannot reuse labels across if-expressions!

• Can’t use same label in two places (invalid assembly)

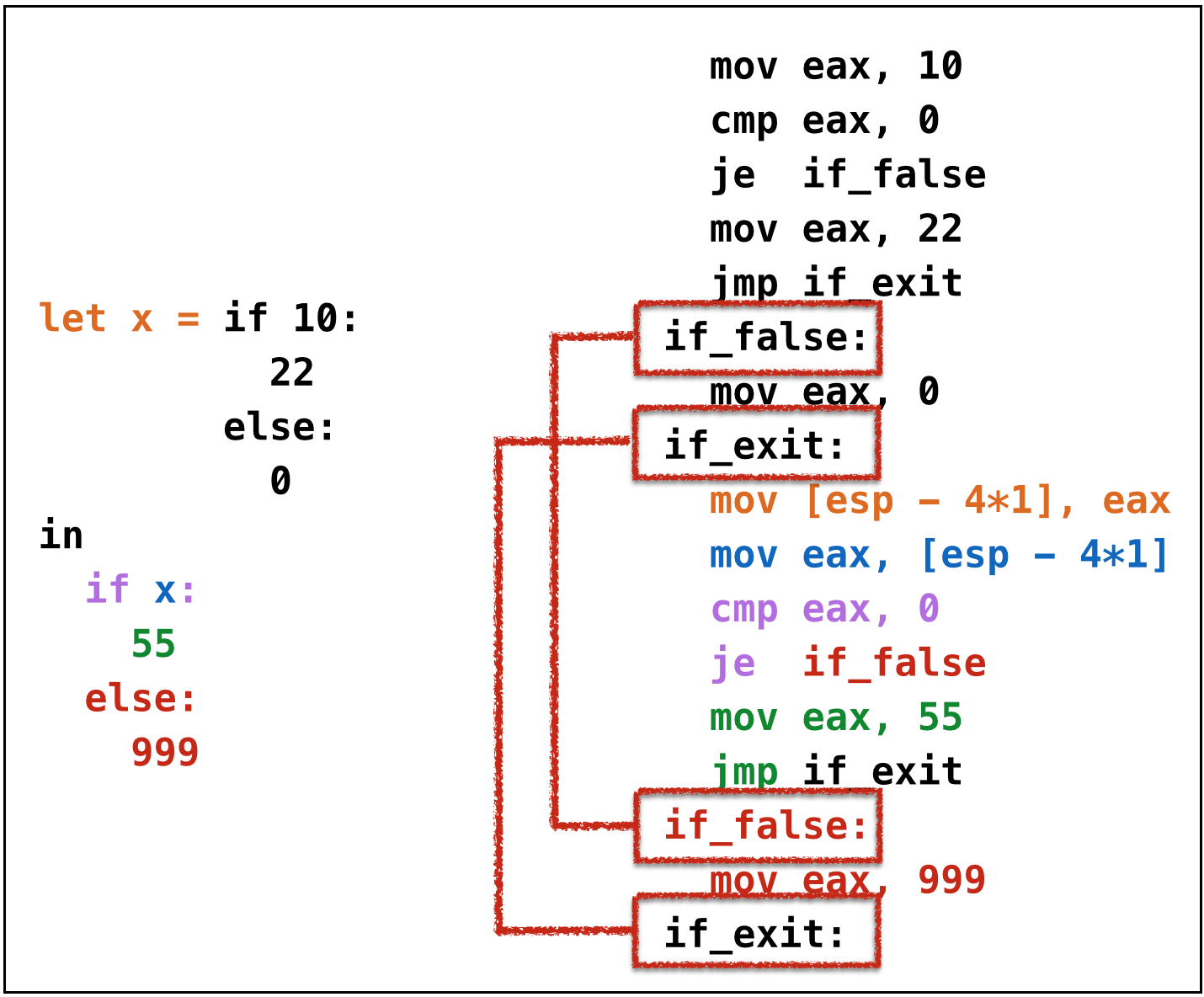
Oops, need distinct labels for each branch!

• Require distinct tags for each if-else expression

Types: Source

Lets modify the Source Expression

data Expr a
  = Number Int                        a
  | Add1   (Expr a)                   a
  | Sub1   (Expr a)                   a
  | Let    Id (Expr a) (Expr a)       a
  | Var    Id                         a
  | If     (Expr a) (Expr a) (Expr a) a

• Add if-else expressions and
• Add tags of type a for each sub-expression
  • Tags are polymorphic a so we can have different types of tags
  • e.g. Source-Position information for error messages

Lets define a name for Tag (just integers).

type Tag   = Int

We will now use:

type BareE = Expr ()     -- AST after parsing
type TagE  = Expr Tag    -- AST with distinct tags

Types: Assembly

Now, lets extend the Assembly with labels, comparisons and jumps:

data Label
  = BranchFalse Tag
  | BranchExit  Tag

data Instruction
  = ...
  | ICmp   Arg   Arg  -- Compare two arguments
  | ILabel Label      -- Create a label
  | IJmp   Label      -- Jump always
  | IJe    Label      -- Jump if equal  
  | IJne   Label      -- Jump if not-equal

Transforms

We can’t expect programmer to put in tags (yuck.)

• Lets squeeze in a tagging transform into our pipeline

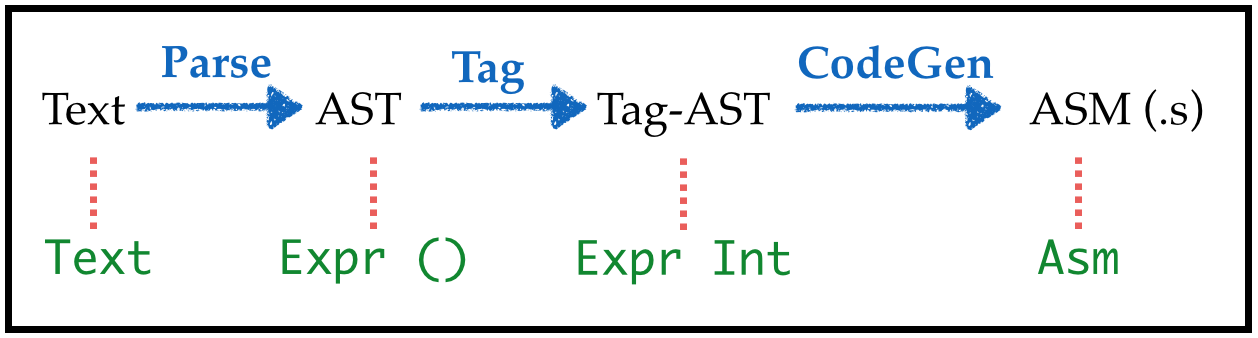
Transforms: Parse

Just as before, but now puts a dummy () into each position

λ> let parseStr s = fmap (const ()) (parse "" s)

λ> let e = parseStr "if 1: 22 else: 33"

λ> e
If (Number 1 ()) (Number 22 ()) (Number 33 ()) ()

λ> label e
If (Number 1 ((),0)) (Number 22 ((),1)) (Number 33 ((),2)) ((),3)

Transforms: Tag

The key work is done by doTag i e

1. Recursively walk over the BareE named e starting tagging at counter i
2. Return a pair (i', e') of updated counter i' and tagged expr e'

QUIZ

doTag :: Int -> BareE -> (Int, TagE)
doTag i (Number n _)    = (i + 1 , Number n i)
doTag i (Var    x _)    = (i + 1 , Var     x i)
doTag i (Let x e1 e2 _) = (_2    , Let x e1' e2' i2)
  where
    (i1, e1')           = doTag i  e1
    (i2, e2')           = doTag _1 e2

What expressions shall we fill in for _1 and _2 ?

{- A -}   _1 = i
          _2 = i + 1

{- B -}   _1 = i
          _2 = i1 + 1

{- C -}   _1 = i
          _2 = i2 + 1

{- D -}   _1 = i1
          _2 = i2 + 1

{- E -}   _1 = i2
          _2 = i1 + 1

(ProTip: Use mapAccumL)

We can now tag the whole program by

• Calling doTag with the initial counter (e.g. 0),

• Throwing away the final counter.

tag :: BareE -> TagE
tag e = e'  where  (_, e') = doTag 0 e

Transforms: CodeGen

Now that we have the tags we lets implement our compilation strategy

compile env (If eCond eTrue eFalse i)
  =   compile env eCond ++              -- compile `eCond`
    [ ICmp (Reg EAX) (Const 0)          -- compare result to 0
    , IJe (BranchFalse i)               -- if-zero then jump to 'False'-block
    ]
   ++ compile env eTrue  ++             -- code for `True`-block
    [ IJmp   lExit      ]               -- jump to exit (don't execute `False`-block!)
   ++
      ILabel (BranchFalse i)            -- start of `False`-block
   : compile env eFalse ++              -- code for `False`-block
    [ ILabel (BranchExit i) ]           -- exit

Recap: Branches

• Tag each sub-expression,
• Use tag to generate control-flow labels implementing branch.

Lesson: Tagged program representation simplifies compilation…

• Next: another example of how intermediate representations help.

Binary Operations

You know the drill.

1. Build intuition with examples,
2. Model problem with types,
3. Implement with type-transforming-functions,
4. Validate with tests.

Compiling Binary Operations

Lets look at some expressions and figure out how they would get compiled.

• Recall: We want the result to be in eax after the instructions finish.

QUIZ

What is the assembly corresponding to 33 - 10 ?

?1 eax, ?2
?3 eax, ?4

mov eax, 33
sub eax, 10

• A. ?1 = sub, ?2 = 33, ?3 = mov, ?4 = 10

• B. ?1 = mov, ?2 = 33, ?3 = sub, ?4 = 10

• C. ?1 = sub, ?2 = 10, ?3 = mov, ?4 = 33

• D. ?1 = mov, ?2 = 10, ?3 = sub, ?4 = 33

How to compile n1 * n2

mov eax, n1
mul eax, n2

Example: Bin1

Lets start with some easy ones. The source:

Strategy: Given n1 + n2

• Move n1 into eax,
• Add n2 to eax.

Example: Bin2

let x = 10        -- position 1 on stack
  , y = 20        -- position 2 on stack
  , z = 30        -- position 3 on stack
in
   x + (y * z)

let x = 10        -- position 1 on stack
  , y = 20        -- position 2 on stack
  , z = 30        -- position 3 on stack
  , tmp = y * z
in
   x + tmp

mov eax, 10
mov [ebp - 4*1], eax    ; put x on stack
mov eax, 20
mov [ebp - 4*2], eax    ; put y on stack
mov eax, 30
mov [ebp - 4*3], eax    ; put z on stack

mov eax, [ebp - 4*2]    ; grab y 
mul eax, [ebp - 4*3]    ; mul by z 
mov [ebp - 4*4], eax    ; put tmp on stack

mov eax, [ebp - 4*1]    ; grab x
add eax, [ebp - 4*4]

What if the first operand is a variable?

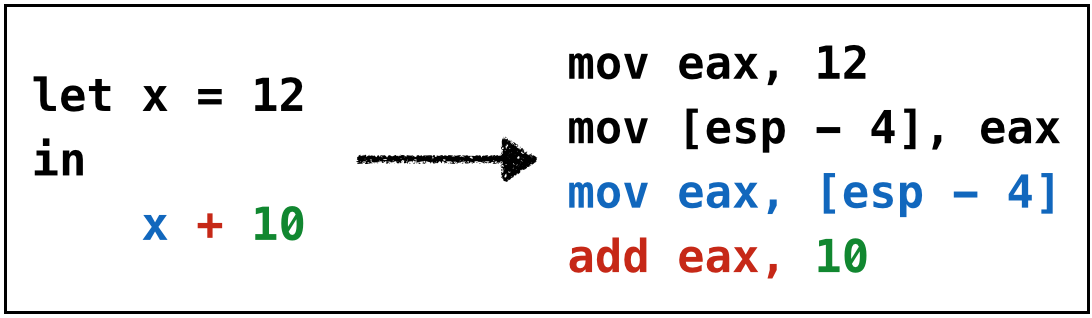
Simple, just copy the variable off the stack into eax

Strategy: Given x + n

• Move x (from stack) into eax,
• Add n to eax.

Example: Bin3

Same thing works if the second operand is a variable.

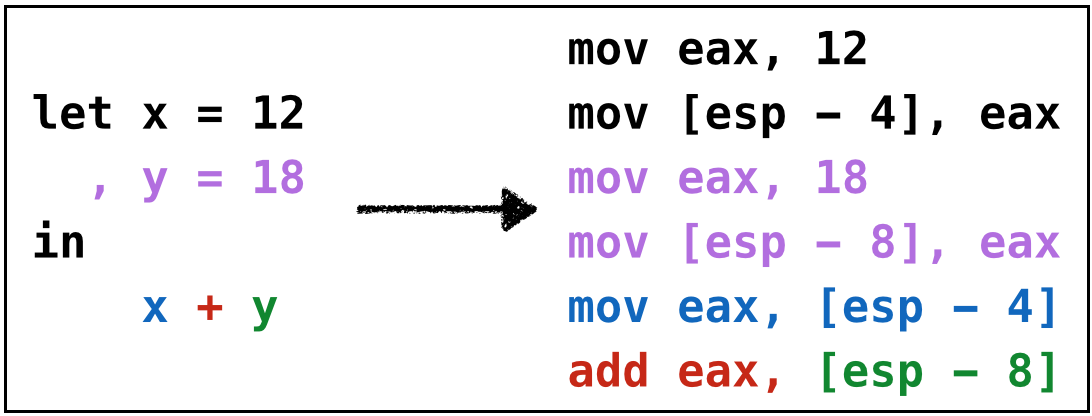
Strategy: Given x + n

• Move x (from stack) into eax,
• Add n to eax.

QUIZ

What is the assembly corresponding to (10 + 20) * 30 ?

mov eax, 10
?1  eax, ?2
?3  eax, ?4

• A. ?1 = add, ?2 = 30, ?3 = mul, ?4 = 20

• B. ?1 = mul, ?2 = 30, ?3 = add, ?4 = 20

• C. ?1 = add, ?2 = 20, ?3 = mul, ?4 = 30

• D. ?1 = mul, ?2 = 20, ?3 = add, ?4 = 30

Second Operand is Constant

In general, to compile e + n we can do

     compile e      
  ++              -- result of e is in eax
     [add eax, n]

Example: Bin4

But what if we have nested expressions

(1 + 2) * (3 + 4)

• Can compile 1 + 2 with result in eax …
• .. but then need to reuse eax for 3 + 4

Need to save 1 + 2 somewhere!

Idea How about use another register for 3 + 4?

• But then what about (1 + 2) * (3 + 4) * (5 + 6) ?
• In general, may need to save more sub-expressions than we have registers.

Idea: Immediate Expressions

Why were 1 + 2 and x + y so easy to compile but (1 + 2) * (3 + 4) not?

Because 1 and x are immediate expressions

Their values don’t require any computation!

• Either a constant, or,
• variable whose value is on the stack.

Idea: Administrative Normal Form (ANF)

An expression is in Administrative Normal Form (ANF)

if all primitive operations have immediate arguments.

Primitive Operations: Those whose values we need for computation to proceed.

• v1 + v2
• v1 - v2
• v1 * v2

QUIZ

Is the following expression in ANF?

(1 + 2) * (4 - 3)

A. Yes, its ANF. B. Nope, its not, because of + C. Nope, its not, because of * D. Nope, its not, because of - E. Huh, WTF is ANF?

isImm :: Expr -> Bool
isImm (Number {}) = True
isImm (Id {})     = True
isImm _           = False

isANF :: Expr -> Bool
isANF (Number {})       = True
isANF (Id {})           = True
isANF (Prim1 _ e1 _)    = isANF e1 -- no need to be `isImm e1`!

isANF (Prim2 _ e1 e2 _) = isImm e1 && isImm e2
isANF (Let _ e1 e2 _)   = isANF e1 && isANF e2
isANF (If e1 e2 e3 _)   = ???   && isANF e2 && isANF e3

A. must be isImm B. meh ANF is fine!

Conversion to ANF

However, note the following variant is in ANF

let t1 = 1 + 2
  , t2 = 3 + 4
in  
    t1 * t2

How can we compile the above code?

; TODO in class

Binary Operations: Strategy

We can convert any expression to ANF

• By adding “temporary” variables for sub-expressions

• Step 1: Compiling ANF into Assembly
• Step 2: Converting Expressions into ANF

Types: Source

Lets add binary primitive operators

data Prim2
  = Plus | Minus | Times

and use them to extend the source language:

data Expr a
  = ...
  | Prim2 Prim2  (Expr a) (Expr a) a

So, for example, 2 + 3 would be parsed as:

Prim2 Plus (Number 2 ()) (Number 3 ()) ()

Types: Assembly

Need to add X86 instructions for primitive arithmetic:

data Instruction
  = ...
  | IAdd Arg Arg
  | ISub Arg Arg
  | IMul Arg Arg

Types: ANF

We can define a separate type for ANF (try it!)

… but …

super tedious as it requires duplicating a bunch of code.

Instead, lets write a function that describes immediate expressions

isImm :: Expr a -> Bool
isImm (Number _ _) = True
isImm (Var    _ _) = True
isImm _            = False

We can now think of immediate expressions as:

The subset of Expr such that isImm returns True

QUIZ

Similarly, lets write a function that describes ANF expressions

isAnf :: Expr a -> Bool
isAnf (Number  _     _) = True
isAnf (Var     _     _) = True
isAnf (Prim2 _ e1 e2 _) = _1
isAnf (If e1 e2 e3   _) = _2
isAnf (Let x e1 e2   _) = _3

What should we fill in for _1?

{- A -} isAnf e1
{- B -} isAnf e2
{- C -} isAnf e1 && isAnf e2
{- D -} isImm e1 && isImm e2
{- E -} isImm e2

QUIZ

Similarly, lets write a function that describes ANF expressions

isAnf :: Expr a -> Bool
isAnf (Number  _     _) = True
isAnf (Var     _     _) = True
isAnf (Prim1 _ e1 _)    = isAnf e1 
isAnf (Prim2 _ e1 e2 _) = isImm e1 && isImm e2 
isAnf (If e1 e2 e3   _) = isANF e1 && isANF e2 && isANF e3
isAnf (Let x e1 e2   _) = isANF e1 && isANF e2 

What should we fill in for _2?

{- A -} isAnf e1      -- <<<<
{- B -} isImm e1      -- <<<<
{- C -} True
{- D -} False

We can now think of ANF expressions as:

The subset of Expr such that isAnf returns True

Use the above function to test our ANF conversion.

immArg :: Env -> ImmExpr -> Arg
immArg env (Number n _) = Const n
immArg env (Id x _)     = RegOffset EBP (lookupEnv env x)

compileImm :: Env -> ImmExpr Tag -> [Instruction]
compileImm env v  = [IMov (Reg EAX) (immArg env v) ]

compile :: Env -> AnfExpr Tag -> [Instruction]
compile env v@(Number {})  = compileImm env v
compile env v@(Id _ _)     = compileImm env v 
compile env (Prim1 op e)   = compile env e
                          ++ [ (prim1Asm op (Reg EAX) (Const 1)]
compile env (Prim2 op v1 v2) = [ compileImm env v1 
                               , prim2asm o (Reg EAX) (immArg env v2) 
                               ]

prim2Asm Add2 = IAdd
prim2Asm Sub2 = ISub
prim2Asm Mul2 = IMul

prim1Asm Add1 = IAdd
prim1Asm Sub1 = ISub


anf :: Int -> Expr a -> (Int, AnfExpr a)
anf i p@(Number {}) = (i, p)
anf i v@(Id {})     = (i, v)
anf i (Prim1 o e)   = (i', Prim1 o e') 
  where 
    (i', e')        = anf i e

anf i (Prim2 o e1 e2) = (i2, mkLet (bs1 ++ bs2) (Prim2 o v1 v2))
  where
     (i1, (bs1, v1))  = imm i  e1
     (i2, (bs2, v2))  = imm i1 e2

anf i (Let x  e1 e2)  = (i2, Let x e1' e2')
  where 
     (i1, e1')        = anf i e1
     (i2, e2')        = anf i1 e2

anf i (If  e1 e2 e3)  = (i3, If e1' e2' e3')
  where 
     (i1, e1')        = anf i e1
     (i2, e2')        = anf i1 e2
     (i3, e3')        = anf i2 e3

imm :: Int -> Expr a -> (Int, ([(Id , AnfExpr a)] , ImmExpr a))
imm i e@(Number {}) = (i, ([], e))
imm i e@(Id {})     = (i, ([], e))
imm i e@(Prim1 {})  = immExp i e
imm i e@(If {})     = immExp i e
imm i e@(Let {})    = immExp i e

imm i (Prim2 o e1 e2) = (i2+1, ((v, Prim2 o v1 v2) : bs2 ++ bs1, Id v))
  where
    (i1, (bs1, v1)) = imm i e1
    (i2, (bs2, v2)) = imm i1 e2
    v               = mkTmpVar i2

mkTmpVar i = "tmp" ++ show i

mkLet :: [(Id , AnfExpr a)] -> AnfExpr a -> AnfExpr a
mkLet []              e = e
mkLet ((x1, e1) : bs) e = Let x1 e1 (mkLet bs e)

immExp i e  = (i' + 1, ([(v, e')], v))
  where
    (i',e') = anf e
    v       = mkTmpVar i'

Types & Strategy

Writing the type aliases:

type BareE   = Expr ()
type AnfE    = Expr ()  -- such that isAnf is True
type AnfTagE = Expr Tag -- such that isAnf is True
type ImmTagE = Expr Tag -- such that isImm is True

we get the overall pipeline:

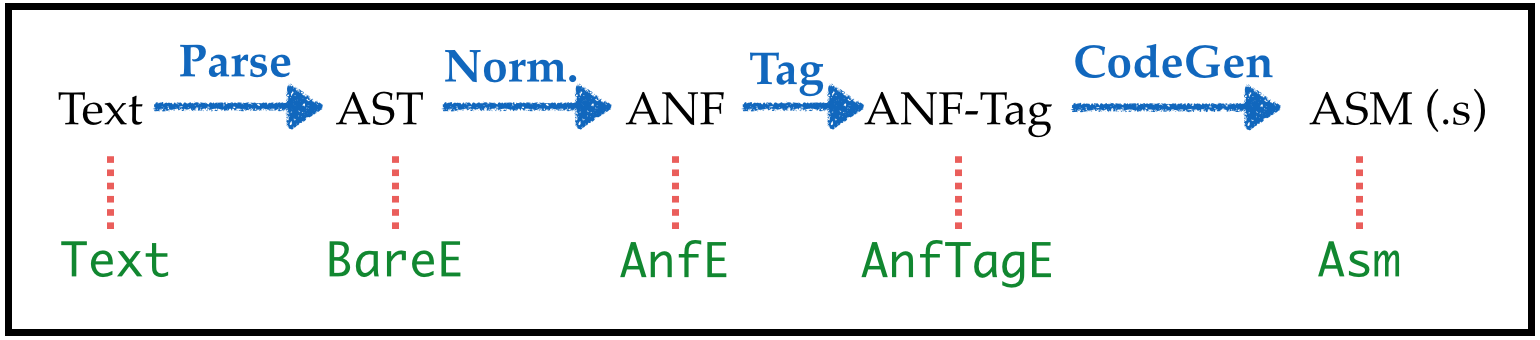
Transforms: Compiling AnfTagE to Asm

The compilation from ANF is easy, lets recall our examples and strategy:

Strategy: Given v1 + v2 (where v1 and v2 are immediate expressions)

• Move v1 into eax,
• Add v2 to eax.

compile :: Env -> TagE -> Asm
compile env (Prim2 o v1 v2)
  = [ IMov      (Reg EAX) (immArg env v1)
    , (prim2 o) (Reg EAX) (immArg env v2)
    ]

where we have a helper to find the Asm variant of a Prim2 operation

prim2 :: Prim2 -> Arg -> Arg -> Instruction
prim2 Plus  = IAdd
prim2 Minus = ISub
prim2 Times = IMul

and another to convert an immediate expression to an x86 argument:

immArg :: Env -> ImmTag -> Arg
immArg _   (Number n _) = Const n
immArg env (Var    x _) = RegOffset ESP i
  where
    i                   = fromMaybe err (lookup x env)
    err                 = error (printf "Error: Variable '%s' is unbound" x)

QUIZ

Which of the below are in ANF ?

{- 1 -} 2 + 3 + 4

{- 2 -} let x = 12 in
          x + 1

{- 3 -} let x = 12
          , y = x + 6
        in
          x + y

{- 4 -} let x = 12
          , y = 18
          , t = x + y + 1
        in
          if t: 7 else: 9

• A. 1, 2, 3, 4

• B. 1, 2, 3

• C. 2, 3, 4

• D. 1, 2

• E. 2, 3

Transforms: Compiling Bare to Anf

Next lets focus on A-Normalization i.e. transforming expressions into ANF

A-Normalization

We can fill in the base cases easily

anf (Number n)      = Number n
anf (Var x)         = Var x

Interesting cases are the binary operations

Example: Anf-1

Left operand is not immediate

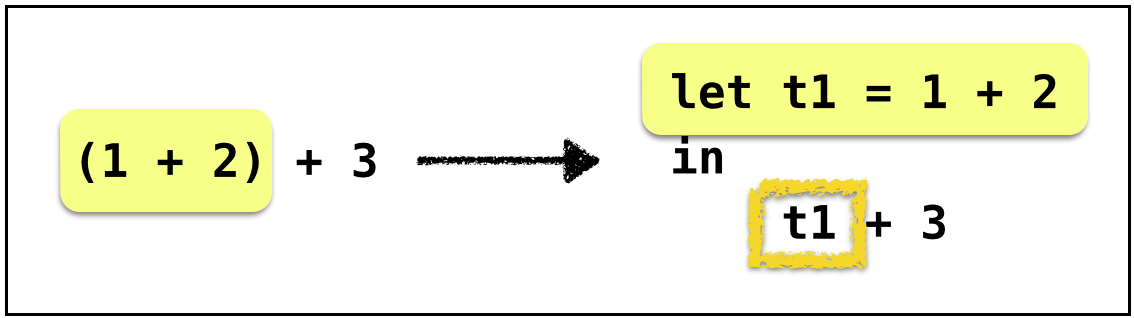
Key Idea: Helper Function

imm :: BareE -> ([(Id, AnfE)], ImmE)

imm e returns ([(t1, a1),...,(tn, an)], v) where

• ti, ai are new temporary variables bound to ANF exprs,
• v is an immediate value (either a constant or variable)

Such that e is equivalent to

let t1 = a1
  , ...
  , tn = an
in
   v

Lets look at some more examples.

Example: Anf-2

Left operand is not internally immediate

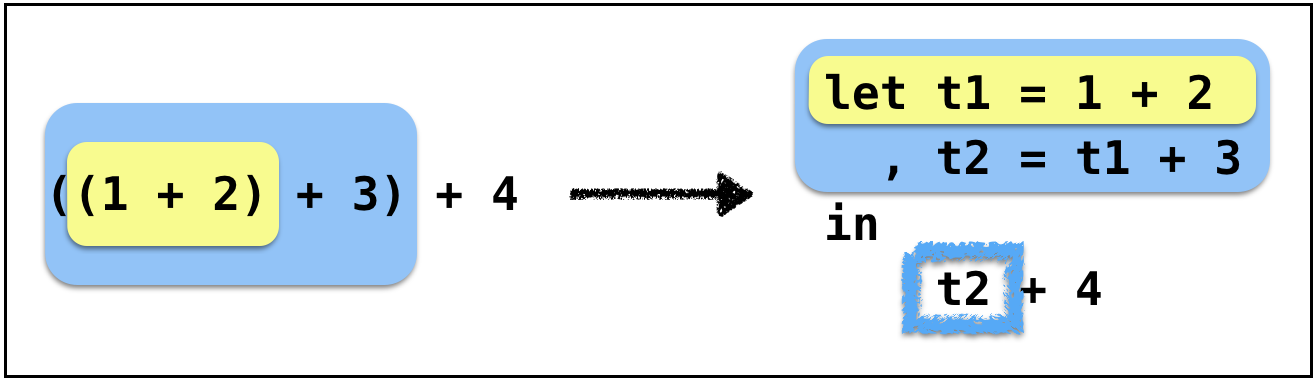
Example: Anf-3

Both operands are not immediate

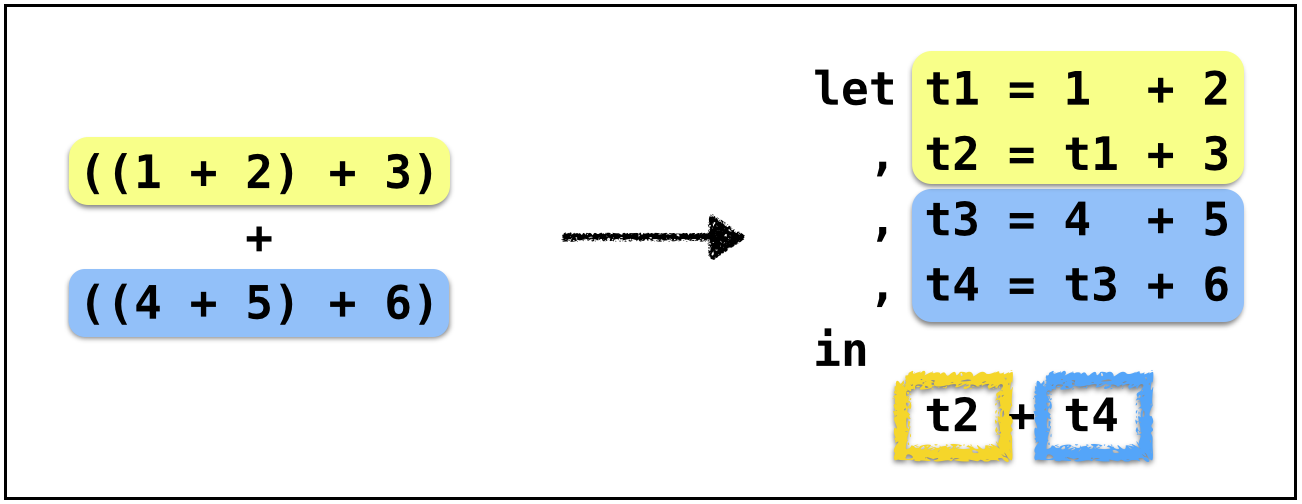
ANF: General Strategy

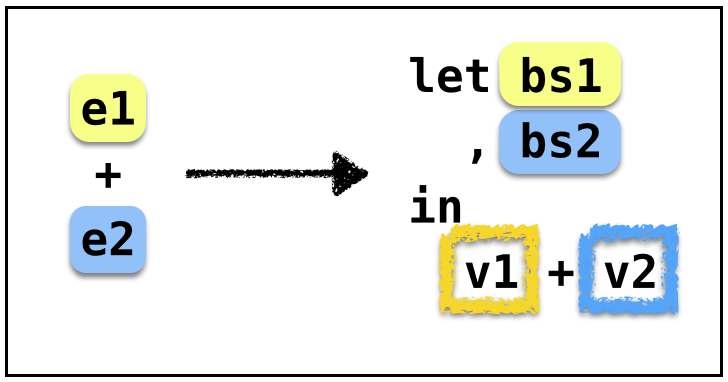
1. Invoke imm on both the operands
2. Concat the let bindings
3. Apply the binop to the immediate values

ANF: Implementation

Lets implement the above strategy

anf (Prim2 o e1 e2) = lets (b1s ++ b2s)
                        (Prim2 o (Var v1) (Var v2))
  where
    (b1s, v1)       = imm e1
    (b2s, v2)       = imm e2

lets :: [(Id, AnfE)] -> AnfE -> AnfE
lets []         e' = e
lets ((x,e):bs) e' = Let x e (lets bs e')

Intuitively, lets stitches together a bunch of definitions as follows:

lets [(x1, e1), (x2, e2), (x3, e3)] e
  ===> Let x1 e1 (Let x2 e2 (Let x3 e3 e))

For Let just make sure we recursively anf the sub-expressions.

anf (Let x e1 e2)   = Let x e1' e2'
  where
    e1'             = anf e1
    e2'             = anf e2

Same principle applies to If

• use anf to recursively transform the branches.

anf (If e1 e2 e3) = If e1' e2' e3'  
  where
    e1'           = anf e1
    e2'           = anf e2
    e3'           = anf e3

ANF: Making Arguments Immediate via imm

The workhorse is the function

imm :: BareE -> ([(Id, AnfE)], ImmE)

which creates temporary variables to crunch an arbitrary Bare into an immediate value.

No need to create an variables if the expression is already immediate:

imm (Number n l) = ( [], Number n l )
imm (Id     x l) = ( [], Id     x l )

The tricky case is when the expression has a primop:

imm (Prim2 o e1 e2) = ( b1s ++ b2s ++ [(t,  Prim2 o v1 v2)]
                      , Id t  )
  t                 = makeFreshVar ()
  (b1s, v1)         = imm e1
  (b2s, v2)         = imm e2  

Oh, what shall we do when:

imm (If e1 e2 e3)   = ???
imm (Let x e1 e2)   = ???

Lets look at an example for inspiration.

That is, simply

• anf the relevant expressions,
• bind them to a fresh variable.

imm e@(If _ _ _) = immExp e
imm e@(If _ _ _) = immExp e

immExp :: AnfE -> ([(Id, AnfE)], ImmE)
immExp e = ([(t, e')], t)
  where
    e'   = anf e
    t    = makeFreshVar ()

One last thing: Whats up with makeFreshVar ?

Wait a minute, what is this magic FRESH ?

How can we create distinct names out of thin air?

What’s that? Global variables? Increment a counter?

We will use a counter, but will have to pass its value around

Just like doTag

anf :: Int -> BareE -> (Int, AnfE)

anf i (Number n l)      = (i, Number n l)

anf i (Id     x l)      = (i, Id     x l)

anf i (Let x e b l)     = (i'', Let x e' b' l)
  where
    (i',  e')           = anf i e
    (i'', b')           = anf i' b

anf i (Prim2 o e1 e2 l) = (i'', lets (b1s ++ b2s) (Prim2 o e1' e2' l))
  where
    (i' , b1s, e1')     = imm i  e1
    (i'', b2s, e2')     = imm i' e2

anf i (If c e1 e2 l)    = (i''', lets bs  (If c' e1' e2' l))
  where
    (i'  , bs, c')      = imm i   c
    (i'' ,     e1')     = anf i'  e1
    (i''',     e2')     = anf i'' e2

and

imm :: Int -> AnfE -> (Int, [(Id, AnfE)], ImmE)

imm i (Number n l)        = (i  , [], Number n l)

imm i (Var x l)           = (i  , [], Var x l)

imm i (Prim2 o e1 e2 l) = (i''', bs, Var v l)
  where
    (i'  , b1s, v1)     = imm i  e1
    (i'' , b2s, v2)     = imm i' e2
    (i''', v)           = fresh i''
    bs                  = b1s ++ b2s ++ [(v, Prim2 o v1 v2 l)]

imm i e@(If _ _ _  l)   = immExp i e

imm i e@(Let _ _ _ l)   = immExp i e

immExp :: Int -> BareE -> (Int, [(Id, AnfE)], ImmE)
immExp i e l  = (i'', bs, Var v ())
  where
    (i' , e') = anf i e
    (i'', v)  = fresh i'
    bs        = [(v, e')]

where now, the fresh function returns a new counter and a variable

fresh :: Int -> (Int, Id)
fresh n = (n+1, "t" ++ show n)

Note this is super clunky. There is a really slick way to write the above code without the clutter of the i but thats too much of a digression, but feel free to look it up yourself

Recap and Summary

Just created Boa with

• Branches (if-expressions)
• Binary Operators (+, -, etc.)

In the process of doing so, we will learned about

• Intermediate Forms
• Normalization

Specifically,