Functions

Next, we’ll build diamondback which adds support for

User-Defined Functions

In the process of doing so, we will learn abou t

Static Checking
Calling Conventions
Tail Recursion

Plan

Defining Functions
Checking Functions
Compiling Functions
Compiling Tail Calls

1. Defining Functions

First, lets add functions to our language.

As always, lets look at some examples.

Example: Increment

For example, a function that increments its input:

def incr(x):
  x + 1

incr(10)

We have a function definition followed by a single “main” expression, which is evaluated to yield the program’s result, which, in this case, is 11.

Example: Factorial

Here’s a somewhat more interesting example:

def fac(n):
  let t = print(n) in
  if (n < 1):
    1
  else:
    n * fac(n - 1)

fac(5)

This program should produce the result

Suppose we modify the above to produce intermediate results:

def fac(n):
  let t   = print(n)
    , res = if (n < 1):
              1
            else:
              n * fac(n - 1)
  in
    print(res)

fac(5)

we should now get:

Example: Mutually Recursive Functions

For this language, the function definitions are global * any function can call any other function.

This lets us write mutually recursive functions like:

def even(n):
  if (n == 0):
    true
  else:
    odd(n - 1)

def odd(n):
  if (n == 0):
    false
  else:
    even(n - 1)

let t0 = print(even(0)),
    t1 = print(even(1)),
    t2 = print(even(2)),
    t3 = print(even(3))
in
    0

QUIZ What should be the result of executing the above?

false true false true 0
true false true false 0
false false false false 0
true true true true 0

Types

Lets add some new types to represent programs.

Bindings

Lets create a special type that represents places where variables are bound,

data Bind a = Bind Id a

A Bind is basically just an Id decorated with an a which will let us save extra metadata like tags or source positions

The metadata will make it easy to report errors.

We will use Bind at two places:

Let-bindings,
Function parameters.

It will be helpful to have a function to extract the Id corresponding to a Bind

bindId :: Bind a -> Id
bindId (Bind x _) = x

Programs

A program is a list of declarations and main expression.

data Program a = Prog
  { pDecls :: [Decl a]    -- ^ function declarations
  , pBody  :: !(Expr a)   -- ^ "main" expression
  }

Declarations

Each function lives is its own declaration,

data Decl a = Decl
  { fName  :: (Bind a)    -- ^ name
  , fArgs  :: [Bind a]    -- ^ parameters
  , fBody  :: (Expr a)    -- ^ body expression
  , fLabel :: a           -- ^ metadata/tag
  }

Expressions

Finally, lets add function application (calls) to the source expressions:

data Expr a
  = ...
  | Let     (Bind a) (Expr a)  (Expr a) a
  | App     Id       [Expr a]           a

An application or call comprises

an Id, the name of the function being called,
a list of expressions corresponding to the parameters, and
a metadata/tag value of type a.

(Note: that we are now using Bind instead of plain Id at a Let.)

Examples Revisited

Lets see how the examples above are represented:

ghci> parseFile "tests/input/incr.diamond"
Prog {pDecls = [Decl { fName = Bind "incr" ()
                     , fArgs = [Bind "n" ()]
                     , fBody = Prim2 Plus (Id "n" ()) (Number 1 ()) ()
                     , fLabel = ()}
               ]
     , pBody = App "incr" [Number 5 ()] ()
     }

ghci> parseFile "tests/input/fac.diamond"
Prog { pDecls = [ Decl {fName = Bind "fac" ()
                , fArgs = [Bind "n" ()]
                , fBody = Let (Bind "t" ()) (Prim1 Print (Id "n" ()) ())
                          (If (Prim2 Less (Id "n" ()) (Number 1 ()) ())
                             (Number 1 ())
                             (Prim2 Times (Id "n" ())
                                (App "fac" [Prim2 Minus (Id "n" ()) (Number 1 ()) ()] ())
                                ()) ()) ()
                , fLabel = ()}
                ]
     , pBody  = App "fac" [Number 5 ()] ()
     }

2. Static Checking

Next, we will look at an increasingly important aspect of compilation, pointing out bugs in the code at compile time

Called Static Checking because we do this without (i.e. before) compiling and running (“dynamicking”) the code.

There is a huge spectrum of checks possible:

Code Linting jslint, hlint
Static Typing
Static Analysis
Contract Checking
Dependent or Refinement Typing

Increasingly, this is the most important phase of a compiler, and modern compiler engineering is built around making these checks lightning fast. For more, see this interview of Anders Hejlsberg the architect of the C# and TypeScript compilers.

Static Well-formedness Checking

We will look at code linting and, later in the quarter, type systems in 131.

For the former, suppose you tried to compile:

def fac(n):
  let t = print(n) in
  if (n < 1):
    1
  else:
    n * fac(m - 1)

fact(5) + fac(3, 4)

We would like compilation to fail, not silently, but with useful messages:

$ make tests/output/err-fac.result

Errors found!

tests/input/err-fac.diamond:6:13-14: Unbound variable 'm'

         6|      n * fac(m - 1)
                         ^

tests/input/err-fac.diamond:8:1-9: Function 'fact' is not defined

         8|  fact(5) + fac(3, 4)      
             ^^^^^^^^

tests/input/err-fac.diamond:(8:11)-(9:1): Wrong arity of arguments at call of fac

         8|  fact(5) + fac(3, 4)
                       ^^^^^^^^^

We get multiple errors:

The variable m is not defined,
The function fact is not defined,
The call fac has the wrong number of arguments.

Next, lets see how to update the architecture of our compiler to support these and other kinds of errors.

Types

An error message type:

data UserError = Error
  { eMsg  :: !Text
  , eSpan :: !SourceSpan
  }
  deriving (Show, Typeable)

We make it an exception (that can be thrown):

instance Exception [UserError]

We can create errors with:

mkError :: Text -> SourceSpan -> Error
mkError msg l = Error msg l

We can throw errors with:

abort :: UserError -> a
abort e = throw [e]

We display errors with:

renderErrors :: [UserError] -> IO Text

which takes something like:

Error
 "Unbound variable 'm'"
 { file      = "tests/input/err-fac"
 , startLine = 8
 , startCol  = 1
 , endLine   = 8
 , endCol    = 9
 }

and produce a pretty message (that requires reading the source file),

tests/input/err-fac.diamond:6:13-14: Unbound variable 'm'

         6|      n * fac(m - 1)
                         ^

We can put it all together by

main :: IO ()
main = runCompiler `catch` esHandle

esHandle :: [UserError] -> IO ()
esHandle es = renderErrors es >>= hPutStrLn stderr >> exitFailure

Which runs the compiler and if any UserError are thrown, catch-es and renders the result.

Transforms

Next, lets insert a checker phase into our pipeline:

In the above, we have defined the types:

type BareP   = Program SourceSpan        -- ^ each sub-expression has source position metadata
type AnfP    = Program SourceSpan        -- ^ each function body in ANF
type AnfTagP = Program (SourceSpan, Tag) -- ^ each sub-expression has unique tag

Catching Multiple Errors

To make using a language and compiler pleasant, we should return as many errors as possible in each run.

Its rather irritating to get errors one-by-one.

We will implement this by writing the functions

wellFormed  :: BareProgram -> [UserError]

which will recursively walk over the entire program, declaration and expression and return the list of all errors.

If this list is empty, we just return the source unchanged,
Otherwise, we throw the list of found errors (and exit.)

Thus, our check function looks like this:

check :: BareProgram -> BareProgram
check p = case wellFormed p of
            [] -> p
            es -> throw es

Well-formed Programs, Declarations and Expressions

The bulk of the work is done by:

wellFormed :: BareProgram -> [UserError]
wellFormed (Prog ds e)
  =  duplicateFunErrors ds
  ++ concatMap (wellFormedD fEnv) ds
  ++ wellFormedE fEnv emptyEnv e
  where
    fEnv  = fromListEnv [(bindId f, length xs)
                          | Decl f xs _ _ <- ds]

This function,

creates fEnv, a map from function-names to the function-arity (number of params),
computes the errors for each declaration (given functions in fEnv),
concatenates the resulting lists of errors.

Traversals

Lets look at how we might find three types of errors:

“unbound variables”
“undefined functions”

(In your assignment, you will look for many more.)

The helper function wellFormedD creates an initial variable environment vEnv containing the functions parameters, and uses that (and fEnv) to walk over the body-expressions.

wellFormedD :: FunEnv -> BareDecl -> [UserError]
wellFormedD fEnv (Decl _ xs e _) = wellFormedE fEnv vEnv e
  where
    vEnv                         = addsEnv xs emptyEnv

The helper function wellFormedE starts with the input vEnv0 (which has just) the function parameters, and fEnv that has the defined functions, and traverses the expression:

At each definition Let x e1 e2, the variable x is added to the environment used to check e2,
At each use Id x we check if x is in vEnv and if not, create a suitable UserError
At each call App f es we check if f is in fEnv and if not, create a suitable UserError.

wellFormedE :: FunEnv -> Env -> Bare -> [UserError]
wellFormedE fEnv vEnv0 e      = go vEnv0 e
  where
    gos vEnv es               = concatMap (go vEnv) es
    go _    (Boolean {})      = []
    go _    (Number  n     l) = []
    go vEnv (Id      x     l) = unboundVarErrors vEnv x l
    go vEnv (Prim1 _ e     _) = go  vEnv e
    go vEnv (Prim2 _ e1 e2 _) = gos vEnv [e1, e2]
    go vEnv (If   e1 e2 e3 _) = gos vEnv [e1, e2, e3]
    go vEnv (Let x e1 e2   _) = go vEnv e1
                             ++ go (addEnv x vEnv) e2
    go vEnv (App f es      l) = unboundFunErrors fEnv f l
                             ++ gos vEnv es

You should understand the above and be able to easily add extra error checks.

QUIZ Which function(s) would we have to modify to add large number errors (i.e. errors for numeric literals that may cause overflow)?

wellFormed :: BareProgram -> [UserError]
wellFormedD :: FunEnv -> BareDecl -> [UserError]
wellFormedE :: FunEnv -> Env -> Bare -> [UserError]
1 and 2
2 and 3

QUIZ Which function(s) would we have to modify to add variable shadowing errors ?

wellFormed :: BareProgram -> [UserError]
wellFormedD :: FunEnv -> BareDecl -> [UserError]
wellFormedE :: FunEnv -> Env -> Bare -> [UserError]
1 and 2
2 and 3

QUIZ Which function(s) would we have to modify to add duplicate parameter errors ?

wellFormed :: BareProgram -> [UserError]
wellFormedD :: FunEnv -> BareDecl -> [UserError]
wellFormedE :: FunEnv -> Env -> Bare -> [UserError]
1 and 2
2 and 3

QUIZ Which function(s) would we have to modify to add duplicate function errors ?

wellFormed :: BareProgram -> [UserError]
wellFormedD :: FunEnv -> BareDecl -> [UserError]
wellFormedE :: FunEnv -> Env -> Bare -> [UserError]
1 and 2
2 and 3

3. Compiling Functions

In the above, we have defined the types:

type BareP   = Program SourceSpan        -- ^ each sub-expression has source position metadata
type AnfP    = Program SourceSpan        -- ^ each function body in ANF
type AnfTagP = Program (SourceSpan, Tag) -- ^ each sub-expression has unique tag

Tagging

The tag phase simply recursively tags each function body and the main expression

ANF Conversion

The normalize phase (i.e. anf) is recursively applied to each function body.
In addition to Prim2 operands, each call’s arguments should be transformed into an immediate expression

Generalize the strategy for binary operators

from (2 arguments) to n-arguments.

Strategy

Now, lets look at compiling function definitions and calls.

We need a co-ordinated strategy for definitions and calls.

Definitions * Each definition is compiled into a labeled block of Asm * That implements the body of the definitions. * (But what about the parameters)?

Calls * Each call of f(args) will execute the block labeled f * (But what about the parameters)?

Strategy: The Stack

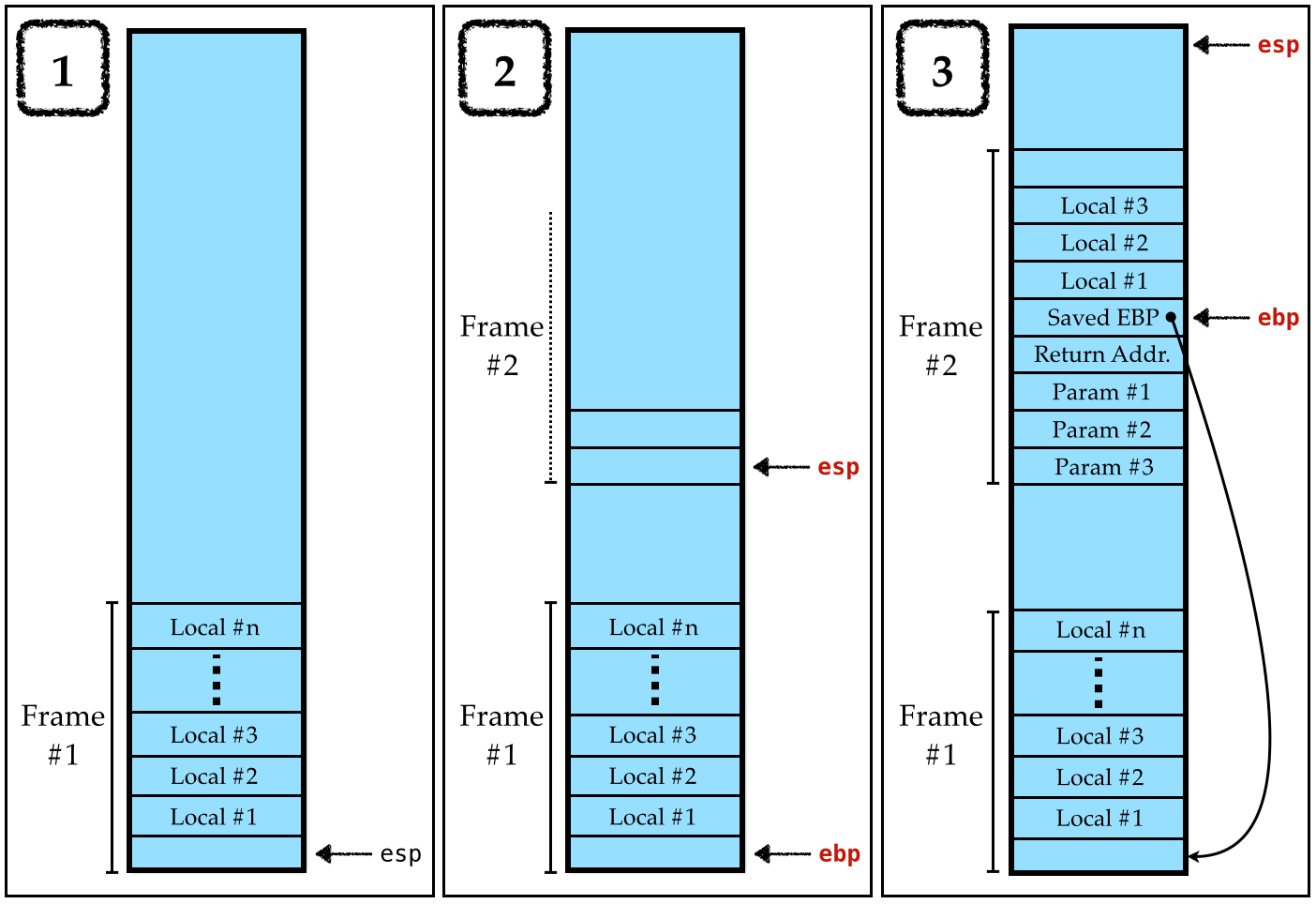
We will use our old friend, the stack to

pass parameters
have local variables for called functions.

Calling Convention

Recall that we are using the C calling convention that ensures the following stack layout:

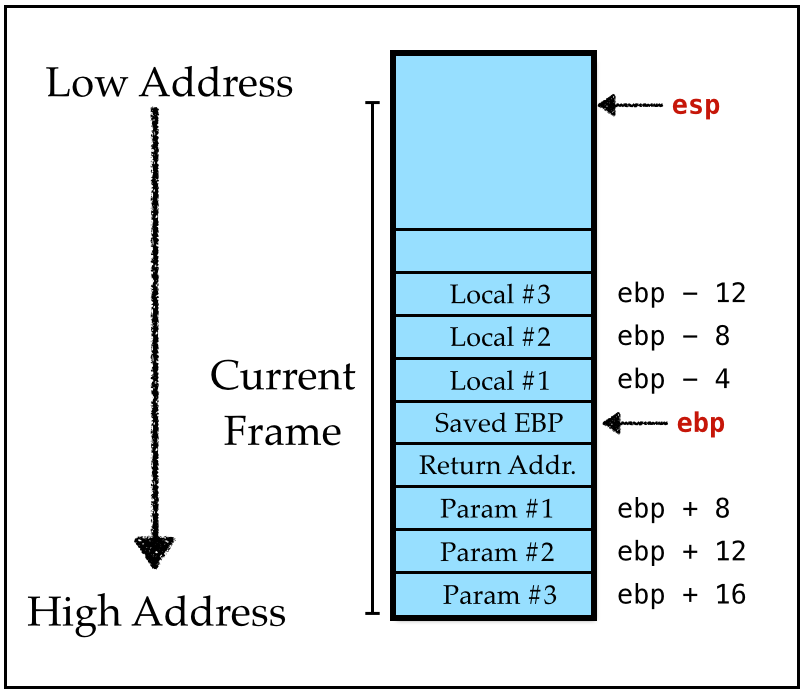
Strategy: Definitions

When the function body starts executing, the parameters x1, x2, … xn are at [ebp + 4*2], [ebp + 4*3], … [ebp + 4*(n+1)].

Ensure that enough stack space is allocated i.e. that esp and ebp are properly managed
Compile body with initial Env mapping parameters to -2, -3,…,-(n+1).

Strategy: Calls

As before we must ensure that the parameters actually live at the above address.

Before the call, push the parameter values onto the stack in reverse order,
Call the appropriate function (using its label),
After the call, clear the stack by incrementing esp appropriately.

NOTE:

At both definition and call, if you are compiling on MacOS, you need to also respect the 16-Byte Stack Alignment Invariant

Types

We already have most of the machinery needed to compile calls.

Lets just add a new kind of Label for each user-defined function:

data Label
  = ...
  | DefFun Id

We will also extend the Arg type to include information about size directives

data Arg
  = ...
  | Sized Size Arg

We will often need to specify that an Arg is a double word
(the other possibilities are – single word and byte) which we needn’t worry about.

data Sized
  = DWordPtr

Implementation

Lets can refactor our compile functions into:

compileProg ::        AnfTagP -> Asm
compileDecl ::        AnfTagD -> Asm
compileExpr :: Env -> AnfTagE -> Asm

that respectively compile Program, Decl and Expr.

In order to simplify stack managment as in Cobra lets have a helper function that compiles the body of each function:

compileBody :: Env -> AnfTagE -> Asm

compileBody env e will wrap the Asm generated by compileExpr env e with the code that manages esp and ebp.

Compiling Programs

To compile a Program we compile each Decl and the main body expression

compileProg (Prog ds e)
  =  compileBody emptyEnv e
  ++ concatMap   compileDecl ds

QUIZ:

Does it matter whether we put the code for e before ds?

QUIZ:

Does it matter what order we compile the ds ?

Compiling Declarations

To compile a single Decl we

Create a block starting with a label for the function’s name (so we know where to call),
Invoke compileBody to fill in the assembly code for the body, using the initial Env obtained from the function’s formal parameters.

compileDecl :: ADcl -> [Instruction]
compileDecl (Decl f xs e _)
  = ILabel (DefFun (bindId f))
  : compileBody (paramsEnv xs) e

The initial Env is created by paramsEnv which returns an Env mapping each parameter to its stack position

paramsEnv :: [Bind a] -> Env
paramsEnv xs = fromListEnv (zip xids [-2, -3..])
  where
    xids     = map bindId xs

(Recall that bindId extracts the Id from each Bind)

Finally, as in cobra, compileBody env e wraps the assmbly for e with the code that manages esp and ebp.

compileBody :: Env -> AnfTagE -> Asm
compileBody env e = entryCode e
                 ++ compileExpr env e
                 ++ exitCode e
                 ++ [IRet]

entryCode :: AnfTagE -> Asm
entryCode e = [ IPush (Reg EBP)
              , IMov  (Reg EBP) (Reg ESP)
              , ISub  (Reg ESP) (Const 4 * n)
              ]
  where
    n       = countVars e

exitCode :: AnfTagE -> Asm
exitCode = [ IMov (Reg ESP) (Reg EBP)
           , IPop (Reg EBP)
           ]

Compiling Calls

Finally, lets extend code generation to account for calls:

compileExpr :: Env -> AnfTagE -> [Instruction]
compileExpr env (App f vs _)
  = call (DefFun f) [param env v | v <- vs]

The function param converts an immediate expressions (corresponding to function arguments)

param :: Env -> ImmE -> Arg
param env v = Sized DWordPtr (immArg env v)

The Sized DWordPtr specifies that each argument will occupy a double word (i.e. 4 bytes) on the stack.

EXERCISE The hard work in compiling calls is done by:

call :: Label -> [Arg] -> [Instruction]

which implements the strategy for calls. Fill in the implementation of call yourself. As an example, of its behavior, consider the (source) program:

def add2(x, y):
  x + y

add2(12, 7)

The call add2(12, 7) is represented as:

App "add2" [Number 12, Number 7]

The code for the above call is generated by

call (DefFun "add2") [arg 12, arg 7]

where arg converts source values into assembly Arg which should generate the equivalent of the assembly:

  push DWORD 14
  push DWORD 24
  call label_def_add2
  add esp, 8

4. Compiling Tail Calls

Our language doesn’t have loops. While recursion is more general, it is more expensive because it uses up stack space (and requires all the attendant management overhead). For example (the python program):

def sumTo(n):
  r = 0
  i = n
  while (0 <= i):
    r = r + i
    i = i - 1
  return r

sumTo(10000)

Requires a single stack frame
Can be implemented with 2 registers

But, the “equivalent” diamond program

def sumTo(n):
  if (n <= 0):
    0
  else:
    n + sumTo(n - 1)

sumTo(10000)

Requires 10000 stack frames …
One for fac(10000), one for fac(9999) etc.

Tail Recursion

Fortunately, we can do much better.

A tail recursive function is one where the recursive call is the last operation done by the function, i.e. where the value returned by the function is the same as the value returned by the recursive call.

We can rewrite sumTo using a tail-recursive loop function:

def loop(r, i):
  if (0 <= i):
    let rr = r + i
      , ii = i - 1
    in
      loop(rr, ii)   # tail call
  else:
    r

def sumTo(n):
  loop(0, n)

sumTo(10000)

Visualizing Tail Calls

Lets compare the execution of the two versions of sumTo

Plain Recursion

sumTo(5)
==> 5 + sumTo(4)
        ^^^^^^^^
==> 5 + [4 + sumTo(3)]
             ^^^^^^^^
==> 5 + [4 + [3 + sumTo(2)]]
                  ^^^^^^^^
==> 5 + [4 + [3 + [2 + sumTo(1)]]]
                       ^^^^^^^^
==> 5 + [4 + [3 + [2 + [1 + sumTo(0)]]]]
                            ^^^^^^^^
==> 5 + [4 + [3 + [2 + [1 + 0]]]]
                        ^^^^^
==> 5 + [4 + [3 + [2 + 1]]]
                   ^^^^^
==> 5 + [4 + [3 + 3]]
              ^^^^^
==> 5 + [4 + 6]
         ^^^^^
==> 5 + 10
    ^^^^^^
==> 15

Each call pushes a frame onto the call-stack;
The results are popped off and added to the parameter at that frame.

Tail Recursion

sumTo(5)
==> loop(0, 5)
==> loop(5, 4)
==> loop(9, 3)
==> loop(12, 2)
==> loop(14, 1)
==> loop(15, 0)
==> 15

Accumulation happens in the parameter (not with the output),
Each call returns its result without further computation

No need to use call-stack, can make recursive call in place. * Tail recursive calls can be compiled into loops!

Tail Recursion Strategy

Instead of using call to make the call, simply:

Move the call’s arguments to the (same) stack position (as current args),
Free current stack space by resetting esp and ebp (as just prior to ret c.f. exitCode),
Jump to the start of the function.

That is, here’s what a naive implementation would look like:

push [ebp - 8]        # push ii
push [ebp - 4]        # push rr
call def_loop

but a tail-recursive call can instead be compiled as:

mov eax , [ebp - 8]  # overwrite i with ii
mov [ebp + 12], eax  
mov eax, [ebp - 4]   # overwrite r with rr
mov [ebp + 8], eax   
mov esp, ebp         # "free" stack frame (as before `ret`)
pop ebp
jmp def_loop         # jump to function start

which has the effect of executing loop literally as if it were a while-loop!

Requirements

To implement the above strategy, we need a way to:

Identify tail calls in the source Expr (AST),
Compile the tail calls following the above strategy.

Types

We can do the above in a single step, i.e., we could identify the tail calls during the code generation, but its cleaner to separate the steps into:

Labeling Expr with Tail Calls — Labeling `Expr` with Tail Calls

In the above, we have defined the types:

type BareP     = Program SourceSpan                 -- ^ each sub-expression has source position metadata
type AnfP      = Program SourceSpan                 -- ^ each function body in ANF
type AnfTagP   = Program (SourceSpan, Tag)          -- ^ each sub-expression has unique tag
type AnfTagTlP = Program ((SourceSpan, Tag), Bool)  -- ^ each call is marked as "tail" or not

Transforms

Thus, to implement tail-call optimization, we need to write two transforms:

1. To Label each call with True (if it is a tail call) or False otherwise:

tails :: Program a -> Program (a, Bool)

2. To Compile tail calls, by extending compileExpr

Labeling Tail Calls

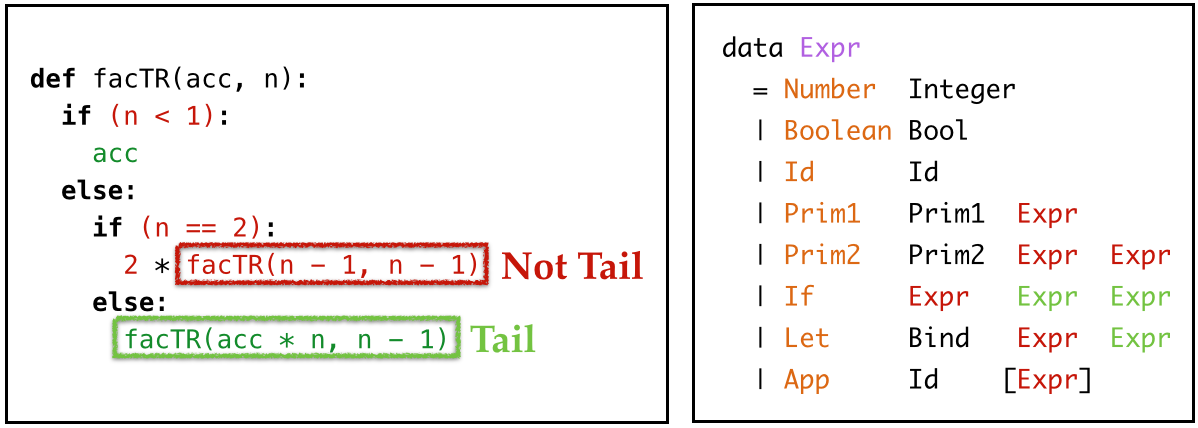
The Expr in non tail positions

Prim1
Prim2
Let (“bound expression”)
If (“condition”)

cannot contain tail calls; all those values have some further computation performed on them.

However, the Expr in tail positions

If (“then” and “else” branch)
Let (“body”)

can contain tail calls (unless they appear under the first case)

Algorithm: Traverse Expr using a Bool

Initially True but
Toggled to False under non-tail positions,
Used as “tail-label” at each call.

NOTE: All non-calls get a default tail-label of False.

tails :: Expr a -> Expr (a, Bool)
tails = go True                                         -- initially flag is True
  where
    noTail l z             = z (l, False)
    go _ (Number n l)      = noTail l (Number n)        
    go _ (Boolean b l)     = noTail l (Boolean b)
    go _ (Id     x l)      = noTail l (Id x)

    go _ (Prim2 o e1 e2 l) = noTail l (Prim2 o e1' e2')
      where
        [e1', e2']         = go False <$> [e1, e2]      -- "prim-args" is non-tail

    go b (If c e1 e2 l)    = noTail l (If c' e1' e2')
      where
        c'                 = go False c                 -- "cond" is non-tail
        e1'                = go b     e1                -- "then" may be tail
        e2'                = go b     e2                -- "else" may be tail

    go b (Let x e1 e2 l)   = noTail l (Let x e1' e2')  
      where
        e1'                = go False e1                -- "bound-expr" is non-tail
        e2'                = go b     e2                -- "body-expr" may be tail

    go b (App f es l)      = App f es' (l, b)           -- tail-label is current flag
      where
        es'                = go False <$> es            -- "call args" are non-tail

EXERCISE: How could we modify the above to only mark tail-recursive calls, i.e. to the same function (whose declaration is being compiled?)

Compiling Tail Calls

Finally, to generate code, we need only add a special case to compileExpr

compileExpr :: Env -> AnfTagTlE -> [Instruction]
compileExpr env (App f vs l)
  | isTail l                 = tailcall (DefFun f) [param env v | v <- vs]
  | otherwise                = call     (DefFun f) [param env v | v <- vs]

That is, if the call is not labeled as a tail call, generate code as before. Otherwise, use tailcall which implements our tail recursion strategy

tailcall :: Label -> [Arg] -> [Instruction]
tailcall f args
  = moveArgs args   -- overwrite current param stack-slots with call args
 ++ exitCode        -- restore ebp and esp
 ++ [IJmp f]        -- jump to start

EXERCISE

Does the above strategy work always? Can you think of situations where it may go horribly wrong?

Recap

We just saw how to add support for first-class function

Definitions, and
Calls

and a way in which an important class of

Tail Recursive functions can be compiled as loops.

Later, we’ll see how to represent functions as values using closures.