Data on the Heap

Next, lets add support for

Data Structures

In the process of doing so, we will learn about

Heap Allocation
Run-time Tags

Creating Heap Data Structures

We have already support for two primitive data types

data Ty
  = TNumber     -- e.g. 0,1,2,3,...
  | TBoolean    -- e.g. true, false

we could add several more of course, e.g.

Char
Double or Float
Long or Short

etc. (you should do it!)

However, for all of those, the same principle applies, more or less

As long as the data fits into a single word (4-bytes)

Instead, we’re going to look at how to make unbounded data structures

Lists
Trees

which require us to put data on the heap (not just the stack) that we’ve used so far.

Pairs

While our goal is to get to lists and trees, the journey of a thousand miles, etc., and so, we will begin with the humble pair.

Semantics (Behavior)

First, lets ponder what exactly we’re trying to achieve. We want to enrich our language with two new constructs:

Constructing pairs, with a new expression of the form (e0, e1) where e0 and e1 are expressions.
Accessing pairs, with new expressions of the form e[0] and e[1] which evaluate to the first and second element of the tuple e respectively.

For example,

let t = (2, 3) in  
  t[0] + t[1]

should evaluate to 5.

Strategy

Next, lets informally develop a strategy for extending our language with pairs, implementing the above semantics. We need to work out strategies for:

Representing pairs in the machine’s memory,
Constructing pairs (i.e. implementing (e0, e1) in assembly),
Accessing pairs (i.e. implementing e[0] and e[1] in assembly).

1. Representation

Recall that we represent all values:

Number like 0, 1, 2 …
Boolean like true, false

as a single word either

4 bytes on the stack, or
a single register eax.

EXERCISE

What kinds of problems do you think might arise if we represent a pair (2, 3) on the stack as:

|     |
-------
|  3  |
-------
|  2  |  
-------
| ... |
-------

QUIZ

How many words would we need to store the tuple

(3, (4, 5))

1 word
2 words
3 words
4 words
5 words

Pointers

Every problem in computing can be solved by adding a level of indirection.

We will represent a pair by a pointer to a block of two adjacent words of memory.

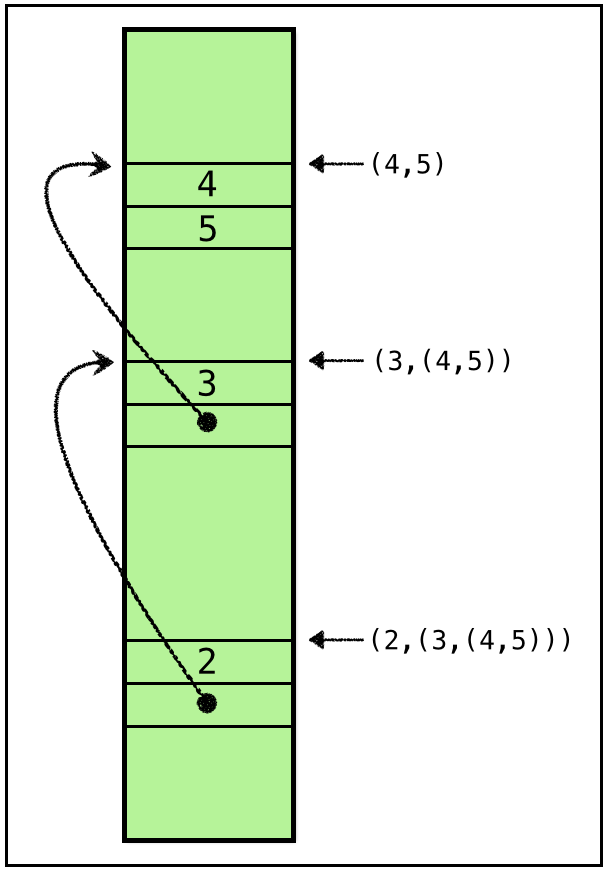
The above shows how the pair (2, (3, (4, 5))) and its sub-pairs can be stored in the heap using pointers.

(4,5) is stored by adjacent words storing

4 and
5

(3, (4, 5)) is stored by adjacent words storing

3 and
a pointer to a heap location storing (4, 5)

(2, (3, (4, 5))) is stored by adjacent words storing

2 and
a pointer to a heap location storing (3, (4, 5)).

A Problem: Numbers vs. Pointers?

How will we tell the difference between numbers and pointers?

That is, how can we tell the difference between

the number 5 and
a pointer to a block of memory (with address 5)?

Each of the above corresponds to a different tuple

(4, 5) or
(4, (...)).

so its pretty crucial that we have a way of knowing which value it is.

Tagging Pointers

As you might have guessed, we can extend our tagging mechanism to account for pointers.

Type	LSB
`number`	xx0
`boolean`	111
`pointer`	001

That is, for

number the last bit will be 0 (as before),
boolean the last 3 bits will be 111 (as before), and
pointer the last 3 bits will be 001.

(We have 3-bits worth for tags, so have wiggle room for other primitive types.)

Address Alignment

As we have a 3 bit tag, leaving 32 - 3 = 29 bits for the actual address. This means, our actual available addresses, written in binary are of the form

Binary	Decimal
0b00000000	0
0b00001000	8
0b00010000	16
0b00011000	24
0b00100000	32
…

That is, the addresses are 8-byte aligned. Which is great because at each address, we have a pair, i.e. a 2-word = 8-byte block, so the next allocated address will also fall on an 8-byte boundary.

2. Construction

Next, lets look at how to implement pair construction that is, generate the assembly for expressions like:

(e1, e2)

To construct a pair (e1, e2) we

Allocate a new 2-word block, and getting the starting address at eax,
Copy the value of e1 (resp. e2) into [eax] (resp. [eax + 4]).
Tag the last bit of eax with 1.

The resulting eax is the value of the pair

The last step ensures that the value carries the proper tag.

ANF will ensure that e1 and e2 are both immediate expressions which will make the second step above straightforward.

EXERCISE How will we do ANF conversion for (e1, e2)?

Allocating Addresses

We will use a global register esi to maintain the address of the next free block on the heap. Every time we need a new block, we will:

Copy the current esi into eax

set the last bit to 1 to ensure proper tagging.
eax will be used to fill in the values

Increment the value of esi by 8

thereby “allocating” 8 bytes (= 2 words) at the address in eax

Note that if

we start our blocks at an 8-byte boundary, and
we allocate 8 bytes at a time,

then

each address used to store a pair will fall on an 8-byte boundary (i.e. have last three bits set to 0).

So we can safely turn the address in eax into a pointer + by setting the last bit to 1.

NOTE: In your assignment, we will have blocks of varying sizes so you will have to take care to maintain the 8-byte alignment, by “padding”.

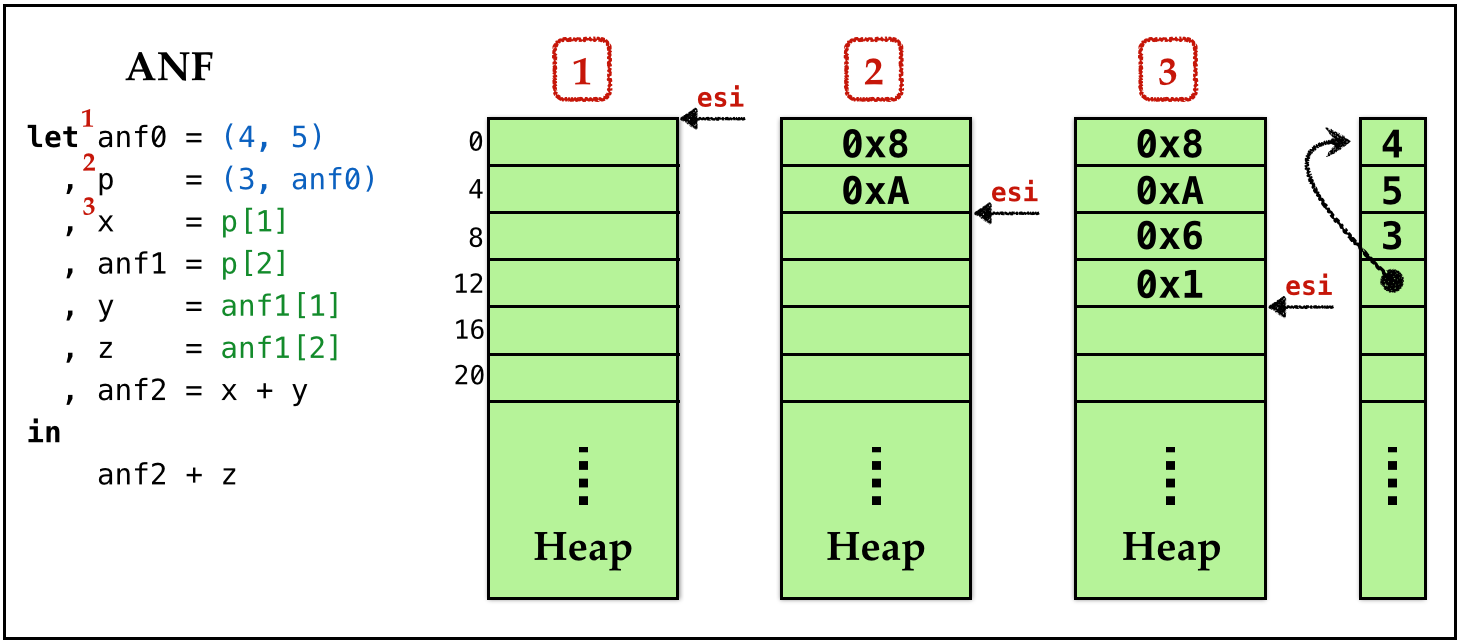
Example: Allocation

In the figure below, we have

a source program on the left,
the ANF equivalent next to it.

The figure below shows the how the heap and esi evolve at points 1, 2 and 3:

QUIZ

In the ANF version, p is the second (local) variable stored in the stack frame. What value gets moved into the second stack slot when evaluating the above program?

0x3
(3, (4, 5))
0x6
0x9
0x10

3. Accessing

Finally, to access the elements of a pair, i.e. compiling expressions like e[0] (resp. e[1])

Check that immediate value e is a pointer
Load e into eax
Remove the tag bit from eax
Copy the value in [eax] (resp. [eax + 4]) into eax.

Example: Access

Here is a snapshot of the heap after the pair(s) are allocated.

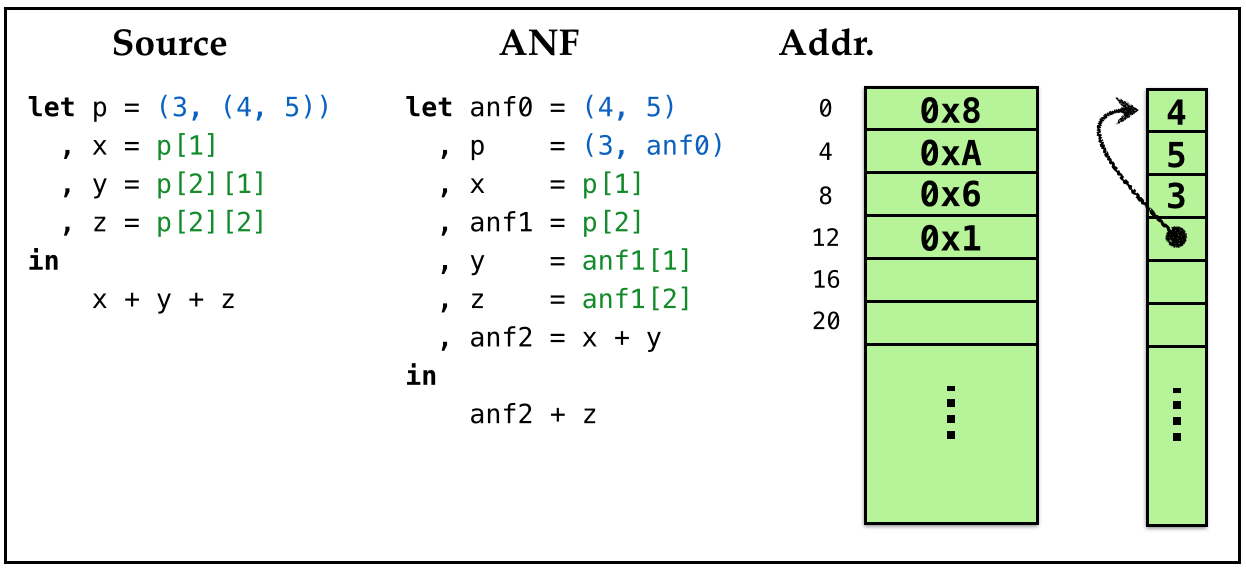
Lets work out how the values corresponding to x, y and z in the example above get stored on the stack frame in the course of evaluation.

Variable	Hex Value	Value
`anf0`	`0x001`	`ptr 0`
`p`	`0x009`	`ptr 8`
`x`	`0x006`	`num 3`
`anf1`	`0x001`	`ptr 0`
`y`	`0x008`	`num 4`
`z`	`0x00A`	`num 5`
`anf2`	`0x00E`	`num 7`
result	`0x018`	`num 12`

Plan

Pretty pictures are well and good, time to build stuff!

As usual, lets continue with our recipe:

Run-time
Types
Transforms

We’ve already built up intuition of the strategy for implementing tuples. Next, lets look at how to implement each of the above.

Run-Time

We need to extend the run-time (c-bits/main.c) in two ways.

Allocate a chunk of space on the heap and pass in start address to our_code.
Print pairs properly.

Allocation

The first step is quite easy we can use calloc as follows:

int main(int argc, char** argv) {
  int* HEAP = calloc(HEAP_SIZE, sizeof (int));
  int result = our_code_starts_here(HEAP);
  print(result);
  return 0;
}

The above code,

Allocates a big block of contiguous memory (starting at HEAP), and
Passes this address in to our_code.

Now, our_code needs to, at the beginning start with instructions that will copy the parameter into esi and then bump it up at each allocation.

Printing

To print pairs, we must recursively traverse the pointers until we hit number or boolean.

We can check if a value is a pair by looking at its last 3 bits:

int isPair(int p) {
  return (p & 0x00000007) == 0x00000001;
}

We can use the above test to recursively print (word)-values:

void print(int val) {
  if(val & 0x00000001 ^ 0x00000001) { // val is a number
    printf("%d", val >> 1);
  }
  else if(val == 0xFFFFFFFF) {       // val is true
    printf("true");
  }
  else if(val == 0x7FFFFFFF) {       // val is false
    printf("false");
  }
  else if(isPair(val)) {            
    int* valp = (int*) (val - 1);    // extract address  
    printf("(");
    print(*valp);                 // print first element
    printf(", ");
    print(*(valp + 1));           // print second element
    printf(")");
  }
  else {
    printf("Unknown value: %#010x", val);
  }
}

Types

Next, lets move into our compiler, and see how the core types need to be extended.

Source

We need to extend the source Expr with support for tuples

data Expr a
  = ...
  | Pair    (Expr a) (Expr a) a   -- ^ construct a pair
  | GetItem (Expr a) Field    a   -- ^ access a pair's element

In the above, Field is

data Field
  = First     -- ^ access first element of pair
  | Second    -- ^ access second element of pair

NOTE: Your assignment will generalize pairs to n-ary tuples using

Tuple [Expr a] representing (e1,...,en)
GetItem (Expr a) (Expr a) representing e1[e2]

Dynamic Types

Let us extend our dynamic types Ty see to include pairs:

data Ty = TNumber | TBoolean | TPair

Assembly

The assembly Instruction are changed minimally; we just need access to esi which will hold the value of the next available memory block:

data Register
  = ...
  | ESI

Transforms

Our code must take care of three things:

Initialize esi to allow heap allocation,
Construct pairs,
Access pairs.

The latter two will be pointed out directly by GHC * They are new cases that must be handled in anf and compileExpr

Initialize

We need to initialize esi with the start position of the heap, that is passed in by the run-time.

How shall we get a hold of this position?

To do so, our_code starts off with a prelude

prelude :: [Instruction]
prelude =
  [ IMov (Reg ESI) (RegOffset 4 ESP)        -- copy param (HEAP) off stack
  , IAdd (Reg ESI) (Const 8)                -- adjust to ensure 8-byte aligned
  , IAnd (Reg ESI) (HexConst 0xFFFFFFF8)    -- add 8 and set last 3 bits to 0
  ]

Copy the value off the (parameter) stack, and
Adjust the value to ensure the value is 8-byte aligned.

QUIZ

Why add 8 to esi? What would happen if we removed that operation?

esi would not be 8-byte aligned?
esi would point into the stack?
esi would not point into the heap?
esi would not have enough space to write 2 bytes?

Construct

To construct a pair (v1, v2) we directly implement the above strategy:

compileExpr env (Pair v1 v2)
  = pairAlloc                        -- 1. allocate pair, resulting addr in `eax`
 ++ pairCopy First  (immArg env v1)  -- 2. copy values into slots
 ++ pairCopy Second (immArg env v2)  
 ++ setTag   EAX     TPair           -- 3. set the tag-bits of `eax`

Lets look at each step in turn.

Allocate

To allocate, we just copy the current pointer esi and increment by 8 bytes,

accounting for two 4-byte (word) blocks for each pair element.

pairAlloc :: Asm
pairAlloc
  = [ IMov (Reg EAX) (Reg ESI)   -- copy current "free address" `esi` into `eax`
    , IAdd (Reg ESI) (Const 8)   -- increment `esi` by 8
    ]

Copy

We copy an Arg into a Field by * saving the Arg into a helper register ebx, * copying ebx into the field’s slot on the heap.

pairCopy :: Field -> Arg -> Asm
pairCopy fld a
  = [ IMov (Reg EBX)    a
    , IMov (pairAddr f) (Reg EBX)
    ]

The field’s slot is either [eax] or [eax + 4] depending on whether the field is First or Second.

pairAddr :: Field -> Arg
pairAddr fld = Sized DWordPtr (RegOffset (4 * fieldOffset fld) EAX)

fieldOffset :: Field -> Int
fieldOffset First  = 0
fieldOffset Second = 1

Tag

Finally, we set the tag bits of eax by using typeTag TPair which is defined

setTag :: Register -> Ty -> Asm
setTag r ty = [ IAdd (Reg r) (typeTag ty) ]

typeTag :: Ty -> Arg
typeTag TNumber  = HexConst 0x00000000    -- last 1 bit  is  0
typeTag TBoolean = HexConst 0x00000007    -- last 3 bits are 111
typeTag TPair    = HexConst 0x00000001    -- last 1 bits is  1

Access

To access tuples, lets update compileExpr with the strategy above:

compileExpr env (GetItem e fld)
  = assertType env e TPair              -- 1. check that e is a (pair) pointer
 ++ [ IMov (Reg EAX) (immArg env e) ]   -- 2. load pointer into eax
 ++ unsetTag EAX TPair                  -- 3. remove tag bit to get address
 ++ [ IMov (Reg EAX) (pairAddr fld) ]   -- 4. copy value from resp. slot to eax

we remove the tag bits by doing the opposite of setTag namely:

unsetTag :: Register -> Ty -> Asm
unsetTag r ty = ISub (Reg EAX) (typeTag ty)

N-ary Tuples

Thats it! Lets take our compiler out for a spin, by using it to write some interesting programs!

First, lets see how to generalize pairs to allow for

triples (e1,e2,e3), —> (e1, (e2, e3))
quadruples (e1,e2,e3,e4), –> (e1, (e2, (e3, e4)))
pentuples (e1,e2,e3,e4,e5)

and so on.

We just need a library of functions in our new egg language to

Construct such tuples, and
Access their fields.

Constructing Tuples

We can write a small set of functions to construct tuples (upto some given size):

def tup3(x1, x2, x3):
  (x1, (x2, x3))

def tup4(x1, x2, x3, x4):
  (x1, (x2, (x3, x4)))

def tup5(x1, x2, x3, x4, x5):
  (x1, (x2, (x3, (x4, x5))))

Accessing Tuples

We can write a single function to access tuples of any size.

So the below code

let yuple = (10, (20, (30, (40, (50, false))))) in 

get(yuple, 0) = 10
get(yuple, 1) = 20
get(yuple, 2) = 30
get(yuple, 3) = 40
get(yuple, 4) = 50




def tup3(x1, x2, x3):
  (x1, (x2, x3))

def tup5(x1, x2, x3, x4, x5):
  (x1, (x2, (x3, (x4, x5))))

let t  = tup5(1, 2, 3, 4, 5) in
  , x0 = print(get(t, 0))
  , x1 = print(get(t, 1))
  , x2 = print(get(t, 2))
  , x3 = print(get(t, 3))
  , x4 = print(get(t, 4))
in
  99

should print out:

How shall we write it?

def get(t, i):
  TODO-IN-CLASS

QUIZ

Using the above “library” we can write code like:

let quad = tup4(1, 2, 3, 4) in
  get(quad, 0) + get(quad, 1) + get(quad, 2) + get(quad, 3)

What will be the result of compiling the above?

Compile error
Segmentation fault
Other run-time error
4
10

QUIZ

Using the above “library” we can write code like:



def get(t, i):
  if i == 0:
    t[0]
  else:
    get(t[1],i-1)

get(t, 2) ===> get(t[1], 1) ===> get(t[1][1], 0)


def tup3(x1, x2, x3):
  (x1, (x2, (x3, false)))

let quad = tup3(1, 2, 3) in
  quad = (1, (2, 3))
  quad[1] = (2, 3)
  quad[1][1] = (3, false)
  quad[1][1][1] = false

  get(quad, 0) + get(quad, 1) + get(quad, 2) + get(quad, 3)

What will be the result of compiling the above?

Compile error
Segmentation fault
Other run-time error
4
10

Lists

Once we have pairs, we can start encoding unbounded lists.

Construct

To build a list, we need two constructor functions:

```python def empty(): false

def cons(h, t): (h, t) ``

We can now encode lists as:

cons(1, cons(2, cons(3, cons(4, empty()))))

Access

To access a list, we need to know

Whether the list isEmpty, and
A way to access the head and the tail of a non-empty list.

def isEmpty(l):
  l == empty()

def head(l):
  l[0]

def tail(l):
  l[1]

Examples

We can now write various functions that build and operate on lists, for example, a function to generate the list of numbers between i and j

def range(i, j):
  if (i < j):
    cons(i, range(i+1, j))
  else:
    emp()

range(1, 5)

which should produce the result

(1,(2,(3,(4,false))))

and a function to sum up the elements of a list:

def sum(xs):
  if (isEmpty(xs)):
    0
  else:
    head(xs) + sum(tail(xs))

sum(range(1, 5))

which should produce the result 10.

Recap

We have a pretty serious language now, with:

Data Structures

which are implemented using

Heap Allocation
Run-time Tags

which required a bunch of small but subtle changes in the

runtime and compiler

In your assignment, you will add native support for n-ary tuples, letting the programmer write code like:

(e1, e2, e3, ..., en)  # constructing tuples of arbitrary arity

e1[e2]                 # allowing expressions to be used as fields

Next, we’ll see how to

use the “pair” mechanism to add higher-order functions and
reclaim unused memory via garbage collection.

data List = Node Int List         -- (Int, List)
          | Empty                 -- false

1:2:3:4:5:6:7:8:[]
(1,(2,(3,(4,(5,(6,(7,(8,false))))))))

def isEmpty(l):
  l == false

def cons(h, t):
  (h, t)

def head(e):
  e[0]

def tail(e):
  e[1]

def length(l):  
  if isEmpty(l):
    0
  else:
    1 + length(tail(l))

data Tree = Node Int Tree Tree    -- (Int, Tree, Tree)
          | Leaf                  -- False

def node(n, l, r):  
  return (n, l, r)

def isLeaf(t):
  t == false

def nodeVal(t)::
  t[0]

def nodeLeft(t)::
  t[1]

def nodeRight(t)::
  t[2]